Cubes & Dice

Important Facts

• A cube has 6 square faces or sides
• A cube has 8 points (vertices)
• A cube has 12 edges
• Only 3 sides of a cube are visible at a time (known as “Joint Sides”) and these sides can never be on the opposite side of each other
• Things that are shaped like a cube are often referred to as ‘cubic’
• Most dice are cube shaped, with the numbers 1 to 6 on the different faces.

Basic Rules for Dice

There are certain dice rules in reasoning which can be used to solve dice-based questions:

Rule No. 1:

Two opposite faces of the dice cannot be adjacent to each other.

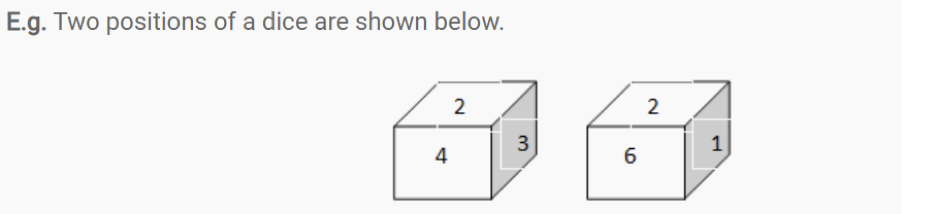
Here, faces with number 4, 3, 6 and 1 are adjacent to the face number 2.
Therefore, the 4, 3, 6, 1 can’t be opposite to the face number 2.
Therefore, face number 5 is opposite to face number 2.

Rule No. 2:

If two dice are as shown below, and one of the two common faces (Face number 4) is in the same position, then the remaining faces will be opposite to each other.

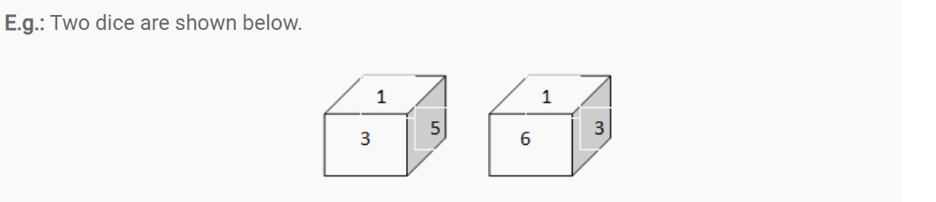
In both the diagrams, two faces numbered 1 & 3 are common.
Also, 5 & 6 are remaining faces. Hence, the face which is number 5 is opposite to the face number 6.

Rule No. 3:

If in 2 different positions of the dice, the positions (different), the position of the face that’s common is the same, and then the opposite faces of the faces that remain will be in the same positions.

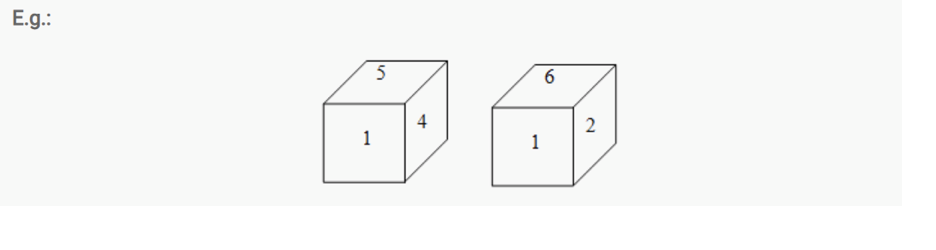
Rule No. 4:

If 2 positions of a die are given (Different) and it is also stated that the common face is different then the face opposite to the given common face would be that which is not shown on any given face in the 2 given positions. It is also to be noted that the opposite face of the faces that are left cannot be the same.

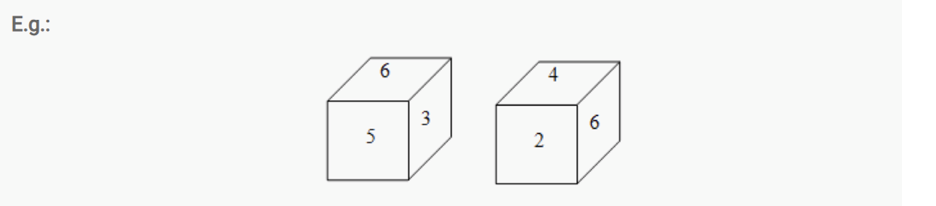
Note, in the above shown dice, the face having value 6 is not in the similar position.

The face numbered 1 is not shown.

So, the face opposite to the face with number 6 is 1. Also, the opposite face of 3 is the face with number 2 and the opposite to face numbered 5 is the face with number 1.

Check out our CSAT Course

Cubes

Following steps must be kept in mind while solving the problems related to painted cubes :

For a cube of side nnn painted on all sides which is uniformly cut into smaller cubes of dimension 111,

• Number of cubes with 0 side painted= (n-2) 3
• Number of cubes with 1 sides painted =6(n - 2) 2
• Number of cubes with 2 sides painted= 12(n-2)
• Number of cubes with 3 sides painted= 8(always)
• For a cuboid of dimension abc painted on all sides which is cut into smaller cubes of dimension 111,
• Number of cubes with 0 side painted= (a-2) (b-2) (c-2)
• Number of cubes with 1 sides painted =2[(a-2) (b-2) + (b-2)(c-2) + (a-2)(c-2) ]
• Number of cubes with 2 sides painted= 4(a+b+c -6)
• Number of cubes with 3 sides painted= 8

Practice Questions

Q1. A cube is painted blue on all faces and is then cut into 125 cubes of equal sizes.
How many cubes are not painted on any faces?
a. 8
b. 16
c. 27
d. 36

Q2. Three opposite different faces of a cube are painted with three different colours - black, yellow, and white. This cube is then cut into 216 smaller but identical cubes. Answer the below questions:
A. Number of small cubes that have exactly three faces painted.
B. How many cubes have two faces painted?
C. How many cubes have only one face painted?
D. What is the number of cubes that have no face painted?

Q3. Each of the six different faces of a cube has been coated with a different colour i.e. V I B G Y and O. Following information is given: (UPSC 2015)
1. Colours Y O and B are on adjacent faces.
2. Colours I G and Y are on adjacent faces.
3. Colours B G and Y are on adjacent faces.
4. Colours O V and B are on adjacent faces.
Which is the colour of the face opposite to the face coloured with “O”?
a. B
b. V
c. G
d. I

Q4. A cuboid has six sides of different colours. The red side is opposite to black. The blue side is adjacent to white. The brown side is adjacent to blue. The red side is face down. Which one of the following would be the opposite to brown? (UPSC 2010)
a. Red
b. Black
c. White
d. Blue

Q5. Six faces of a cube are numbered from 1 to 6, each face carrying one different number. Further,
1. The face 2 is opposite to the face 6.
2. The face 1 is opposite to the face 5.
3. The face 3 is between the face 1 and the face 5
4. The face 4 is adjacent to the face 2.
Which one of the following is correct?
a. The face 2 is adjacent to the face 3
b. The face 6 is between the face 2 and the face 4
c. The face 1 is between the face 5 and the face 6
d. None of the above

6. Each face of a cube can be painted in black or white colours. In how many different ways can the cube be painted? (UPSC 2019)
a. 9
b. 10
c. 11
d. 12

7. A solid cube of 3 cm side, painted on all its faces, is cut up into small cubes of 1 cm side. How many of the small cubes will have exactly two painted faces?
(UPSC 2018)
a. 12
b. 8
c. 6
d. 4

8. A large cube has all its faces painted with different colours. It is cut into smaller cubes of equal sizes such that the side of the small cube is one-fifth the side of the large cube. The number of small cubes with at least two colours on its body is:
a. 54
b. 44
c. 36
d. 27

9. A cube has all its faces painted with different colours. It is cut into smaller cubes of equal sizes such that the side of the small cube is one-fourth the big cube. The number of small cubes with only one of the sides painted is: (UPSC 2016)
a. 32
b. 24
c. 16
d. 8

10. A cube has six numbers marked 1,2,3,4,5 and 6 on it’s faces. Three views of the cube are shown below: (UPSC 2013)

What possible number can exist on the two faces marked and respectively on the cube?

a. 2 and 3
b. 6 and 1
c. 1 and 4
d. 3 and 1

11. All the faces of a cube are painted with blue colour. Then it is cut into 125 small equal cubes. How many small cubes will be formed having no face coloured ?
a. 27
b. 8
c. 16
d. 24

12. A solid cube is painted yellow, blue and black such that opposite faces are of same colour. The cube is then cut into 36 cubes of two different sizes such that 32 cubes are small and the other four cubes are Big. None of the faces of the bigger cubes is painted blue. How many cubes have only one face painted? (UPSC 2019)
a. 4
b. 6
c. 8
d. 10

13. If all the faces of a cube are painted, and 9 cuts are made on it, such that the cube gets divided into maximum number of identical cubes. How many small cubes will not have any painted faces?
a. 4
b. 8
c. 27
d. 36

To view the answer keys, register yourself at UPSCprep.com