Number System

Core Concepts

1. Number line: It is one of the most crucial concepts in Basic Numeracy. The number line is a straight line between negative infinity on the left to positive infinity to the right.

2. Important Mathematical Representations

• Even numbers: 2n
• Odd Numbers: 2n-1
• Numbers multiple of 4: 4n, and so on

3. Prime Factors: Representation of numbers in the standard form.

4. Standard Form or Canonical Form: eg. Finding standard form of 144

Therefore, Prime factors of 144= 2 * 2 * 2 * 2 * 3 * 3 = 2^4 * 3^2

5. General Form for Writing 2-3 Digit Numbers: In mathematics many a time we have to use algebraic equations in order to solve questions. In such cases an important concept is the way we represent two or three-digit numbers in equation form. For instance, suppose we have a 2-digit number with the digits ‘AB’. In order to write this in the form of an equation, we have to use:
   10A + B. This is because in the number ‘AB’ the digit A is occupying the tens place. Hence, in order to represent the value of the number ‘AB’ in the form of an equation — we can write 10A + B.
   Thus, the number 29 = 2 * 10 + 9 * 1

6. Similarly, for a three-digit number with the digits A, B and C respectively — the number ‘ABC’ can be represented as below:
   ABC = 100A+10B+C
   Thus, 243 = 2 * 100 + 4 * 10 + 3 * 1

7. The BODMAS Rule: It is used for the ordering of mathematical operations in a mathematical situation. In any mathematical situation, the first thing to be considered is Brackets followed by Division, Multiplication, Addition and Subtraction in that order.

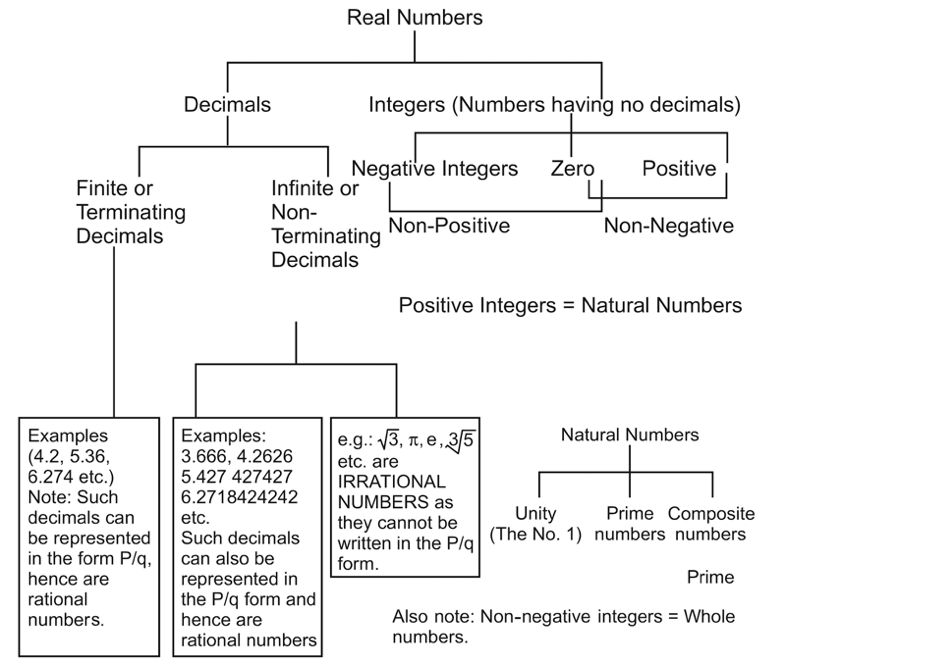
Number System

• Integers: Numbers having no decimal point in it
  • Positive Integers - 1, 2, 3, …
  • Zero
  • Negative Integers: -1, -2, -3, …
• Decimals: A decimal number is a number with a decimal point in it, like these: 1.5, 3.21, 4.173, 5.1, etc.
• Natural numbers: These are the numbers (1, 2, 3, etc.) that are used for counting. In other words, all positive integers are natural numbers. Based on divisibility, there could be two types of natural numbers: Prime and Composite.
  • Prime numbers - A natural number larger than unity is a prime number if it does not have other divisors except for itself and unity. (Note: Unity (i.e. 1) is not a prime number.)
  • Composite Numbers: It is a natural number that has at least one divisor different from unity and itself.
    Every composite number n can be factored into its prime factors. (This is sometimes called the canonical form of a number.)
• Whole Numbers: The set of numbers that includes all natural numbers and the number zero are called whole numbers. Whole numbers are also called non-negative integers.
• Real Numbers: All numbers that can be represented on the number line are called real numbers.
• Rational Numbers: A rational number is defined as a number of the form a/b where a and b are integers and b ⧣ 0.
• Irrational numbers: Fractions, that are non-terminating, non-periodic fractions, are irrational numbers. Some examples of irrational numbers are √2, √3, √5, e, pi, etc.
• Co-prime numbers are any two numbers which have an HCF of 1, i.e. when two numbers have no common prime factor apart from the number 1, they are called co-prime or relatively prime to each other. Eg. (5, 6), (29,30)

---

Operations on Numbers

1. Exponents and Powers

• Exponents, or powers, are an important part of maths as they are necessary to indicate that a number is multiplied by itself for a given number of times.

• When a number is multiplied by itself it gives the ‘square of the number’. Thus,

• n * n = n^2 (e g. 3 * 3 = 3^2)

• If the same number is multiplied by itself twice we get the cube of the number. Thus, n * n * n= n^3 (e g. 3 * 3 * 3= 3^3)
  n * n * n * n= n^4 and so on.

• With respect to powers of numbers, there are 5 basic rules which you should know: For any number ‘n’ the following rules would apply:

  • Rule 1: n^a × n^b = n^(a+b). Thus, 4^3 × 4^5 = 4^(3+5) = 4^8
  • Rule 2: n^a / n^b = n^(a-b). Thus, 3^9 / 3^4 = 3^5.
  • Rule 3: n^ (a^b)= n^(a×b). Thus, 3^ (2^4 )= 3^8.
  • Rule 4: n^ (-a) = 1/n^a . Thus, 3^ (-4)=1/3^(4)
  • Rule 5: n^0=1. Thus, 5^0=1.

These are also popularly known as the rules of indices.

2. Properties

• Commutative property of addition: a + b = b + a.
• Associative property of addition: (a + b) + c = a + (b + c).
• Commutative property of multiplication: ab = ba.
• Associative property of multiplication: (ab) * c= a(b*c).
• Distributive property of multiplication with respect to addition: (a + b) c = ac + bc.
• Subtraction and division are defined as the inverse operations to addition and multiplication respectively.

LCM and HCF

LCM (Least Common Multiple)

• Smallest natural number 'n' which is divisible by n1 & n2
  How to find LCM?
• Find Standard forms of n1, n2
• Write down all prime factors
• Raise each prime factor to highest of the powers
• The product will be LCM

Eg. Find the LCM of 150, 210.

• Step 1: Writing down the standard form of numbers
  • 150 = 5 * 5 * 3 * 2
  • 210 = 5 * 2 * 7 * 3
• Step 2: Write down all the prime factors: that appear at least once in any of the numbers: 5, 3, 2, 7.
• Step 3: Raise each of the prime factors to their highest available power (considering each to the numbers).
  • The LCM= 2^1 * 3^1 * 5^2 * 7= 2 * 3 * 25 * 7 = 1050

Highest Common Factor (HCF)

• For n1, n2: If n1 and n2 are exactly divisible by the same number x, then x is a common divisor (CD) of n1, n2. Highest of all such CDs of n1 and n2 is HCF.

How to find HCF?

• Find Standard forms of n1, n2
• Write down all prime factors
• Find Common factors in both n1, n2.
• Raise each prime factor to lesser of the powers
• The product will be HCF

E.g., Find the HCF of 150, 210, 375.

• Step 1: Writing down the standard form of numbers
  • 150 = 5 * 5 * 3 * 2
  • 210 = 5 * 2 * 7 * 3
• Step 2: Writing Prime factors common to all the numbers: 5, 2, 3 (Note: we didn’t consider 7 as it is only a common factor of 210 and not of 150!)
• Step 3: Raising each prime factor to lesser of the power, i.e.- 2^1, 5^1 and 3^1
• Step 4: Hence, the HCF will be 2 * 5 * 3 = 30

Important Rule:
HCF (n1, n2) * LCM (n1, n2) = n1*n2
i.e., The product of the HCF and the LCM equals the product of the numbers.

Rule for finding out HCF and LCM of fractions
HCF of two or more fractions is given by:

• LCM of two or more fractions is given by:

The Remainder Theorem

• Remainder of a division or expression can be expressed as positive and negative numbers, though negative numbers cannot be remainders. But we can use them, to find out the correct remainder easily.
• Consider following expression,
• 107/9, here remainder is positive remainder is +8, and negative remainder is 8-9 = -1.
• This method helps in finding the reminders for large expressions, refer to the example given below.
  (1753 * 1749 * 83 * 171 / 17)
  Remainders for each number in the numerator,
  (+2 * -2 * -2 * 1)/17 = 8/17
  Hence, remainder is 8.

---

CSAT 360 Course for Prelims 2024

• Complete coverage of all CSAT Topics - Maths, Logical Reasoning, Language comprehension, etc.
• Comprehensive CSAT Workbook - one stop source for CSAT - theory + formulae + practice question sets. 
• Live classes from Monday to Saturday - with Recording access for 3 years
• 5 CSAT Full length Tests
• Practice MCQs after each lecture
• Special Live Practice Sessions - Practice CSAT in live session with faculty

---

CSAT Topics

1. 🔢 CSAT Mathematics
2. 🧠 CSAT Logical Reasoning
3. 📋

---

Practice Questions

1. The LCM of two numbers is 936. If their HCF is 4 and one of the numbers is 72, the other is:
a. 42
b. 52
c. 62
d. None of these

2. Two alarm clocks ring their alarms at regular intervals of 50 seconds and 48 seconds. If they first beep together at 12 noon, at what time will they beep again for the first time
a.12:10 PM
b.12:12 PM
c.12:11 PM
d. None of these

3. Integers are listed from 700 to 1000. In how many integers is the sum of the digits 10?
(UPSC 2021)
a. 6
b. 7
c. 8
d. 9

4. Two equilateral triangles have the sides of lengths 34 and 85, respectively. The greatest length of tape that can measure both of them exactly is:
a.18
b.16
c.17
d.15

5. The number of integers n satisfying – n + 2 ≥ 0 and 2n ≥ 4 is:
a. 0
b. 1
c. 2
d. 3

6. A teacher teaching students of third standard gave a simple multiplication exercise to the kids. But one kid reversed the digits of both the numbers and carried out the multiplication and found that the product was exactly the same as the one expected by the teacher. Only one of the following pairs of numbers will fit in the description of the exercise. Which one is that?
a. 14,22
b. 26,62
c. 19,33
d. 42,28

7. 273 –272 –271 is the same as
a. 269
b. 270
c. 271
d. 272

8. How many zeroes are there at the end of the following product?
1 × 5 × 10 × 15 × 20 × 30 × 35 × 40 × 45 × 50 × 55 × 60 (UPSC 2020)
a. 10
b. 12
c. 14
d. 15

9. The number 3798125P369 is divisible by 7. What is the value of the digit P?
(UPSC 2021)
a. 1
b. 6
c. 7
d. 9

10. Find the remainder when 73+75+78+57+197 is divided by 34.
a. 4
b. 5
c. 6
d. 8

11. The last digit of the number obtained by multiplying the numbers 81 82 * 83 * 84 * 85 * 86 * 87 * 88 * 89 will be:*
a. 0
b. 6
c. 7
d. 2

12. Consider the following sequence of numbers: 5 1 4 7 3 9 8 5 7 2 6 3 1 5 8 6 3 8 5 2 2 4 3 4 9 6. How many odd numbers are followed by an odd number in the above sequence? (UPSC 2020)
a. 5
b. 6
c. 7
d. 8

13. In a school, every student is assigned a unique identification number. A student is a football player if and only if the identification number is divisible by 4, whereas a student is a cricketer if and only if the identification number is divisible by 6. If every number from 1 to 100 is assigned to a student, then how many of them play cricket as well as football?
a. 4
b. 8
c. 10
d. 12

14. The sum of two integers is 10 and the sum of their reciprocals is 5/12. The integers are?
a. 7,3
b. 9,1
c. 8,2
d. 6,5

15. Three times the first of three consecutive odd integers are 3 more than twice the third. Find the value of the third integer.
a. 9
b. 11
c. 13
d. 15

16. If 381A is divisible by 9, find the value of smallest natural number A.
a. 5
b. 8
c. 7
d. 6
e. 6

17. What is the remainder of 3^2019 when divided by 10? (UPSC 2021)
a.1
b.3
c.7
d.9

18. What is the remainder when 1421 * 1423 * 1425 is divided by 12?
a. 0
b. 9
c. 3
d. 6

19. A biology class at Central High School predicted that a local population of animals will double in size every 12 years. The population at the beginning of 2014 was estimated to be 50 animals. If P represents the population n years after 2014, then which of the following equations represents the class's model of the population over time? (UPSC 2021)
a. P= 12+50n
b. P=12n+50
c. P= 50* 2^12n
d. P = 50 * 2^(n/12)

20. The sides of a hexagonal field are 216, 423, 1215, 1422, 2169 and 2223 metres. Find the greatest length of tape that would be able to exactly measure each of these sides without having to use fractions/parts of the tape?
a. 18
b. 54
c. 27
d. 9

21. Let XYZ be a three-digit number, where (X + Y + Z) is not a multiple of 3. Then (XYZ + YZX + ZXY) is not divisible by: (UPSC 2020)
a. 3
b. 9
c. 37
d. (X+Y+Z)

22. Let p, q, r and s be natural numbers such that p - 2016 = q + 2017 = r - 2018 = s + 2019 Which one of the following is the largest natural number? (UPSC 2020)
a. p
b. q
c. r
d. s

23. In the sum ⊗ + 1 ⊗ + 5 ⊗ + ⊗ ⊗ + ⊗ 1 = 1 ⊗ ⊗ for which digit does the symbol ⊗ stand? (UPSC 2020)
a. 2
b. 3
c. 4
d. 5

24. One page is torn from a booklet whose pages are numbered in the usual manner starting from the first page as 1. The sum of the numbers on the remaining pages is 195. The torn page contains which of the following numbers. (UPSC 2020)
a. 5, 6
b. 7, 8
c. 9, 10
d. 11,12

25. Find the smallest 3-digit number which divided by 5 gives remainder 2.
a. 100
b. 102
c. 104
d. 105

26. If the numerator and denominator of a proper fraction are increased by the same quantity, then the resulting fraction is? ( UPSC 2019)
a. always less than the original fraction
b. always greater than the original fraction
c. always equal to the original fraction
d. such that nothing can be claimed definitely

27. The number of times the digit 5 will be written when listing the integers from 1 to 1000, is (UPSC 2019)
a. 269
b. 271
c. 300
d. 302

28. Four-digit numbers are to be formed using the digit 1, 2, 3, and 4; and none of these four digits are repeated in any manner further, (UPSC 2016)
1. 2 and 3 are not to immediately follow each other
2. 1 is not to be immediately follow by 3
3. 4 is not appear at the last place
4. 1 is not appear at the first place
How many different numbers can be formed?
a. 6
b. 8
c. 9
d. None of above

29. consider the following statement in respect of two natural numbers p and q such that p is a prime number and q is a composite number: (UPSC 2022)
1. p * q can be an odd number.
2. p / q can be a prime number.
3. p + q can be a prime number.
Which of the above statement are correct?
a. 1 and 2 only
b. 2 and 3 only
c. 1 and 3 only
d. 1, 2, and 3

30. While writing all the numbers from 700 to 1000, how many numbers occur in which the digit at hundred’s place is greater than the digit at ten’s place is greater than the digit at unit’s place?
(UPSC 2018)
a. 61
b. 64
c. 85
d. 91

31. Find the greatest number of 5 digits, that will give us a remainder of 5, when divided by 8 and 9, respectively.
a. 99931
b. 99941
c. 99725
d. None of these

32. A zoo had some lions and some parrots. The kipper counted 15 heads and 50 legs. The number of lions in the zoo are
a. 9
b. 10
c. 8
d. 11

33. Find the greatest 6 – digit number, which multiple of 12?
a. 999980
b. 999990
c. 999984
d. None of these

34. The HFC of two number is 11, and their LCM is 624. If one of the numbers is 88, find the other.
a. 78
b. 87
c. 97
d. None of these

35. Find the smallest number which leaves 22, 35, 48, and 61 as remainders when divided by 26,39,52 and 65 respectively.
a. 760
b. 776
c. 766
d. 780
e. None of these

Log-in to access answers for Number systems and other topics!

If you have made it so far, well done. You are ahead of the competition.

Best of luck!