Set Theory

Introduction

Set theory is the mathematical theory of well-determined collections, called sets. These sets can be of objects that are called members, or elements, of the set.

• Sets: A set is a collection of distinct objects, called elements of the set.
  E.g., A is the set of all even numbers
  A= [2, 4, 6, ……….]
• A set simply specifies the contents; order/sequence is not important. The set represented by {1, 2, 3} is equivalent to the set {3, 1, 2}
• A set that contains no elements, { }, is called the empty set (or Null set) and is notated ∅
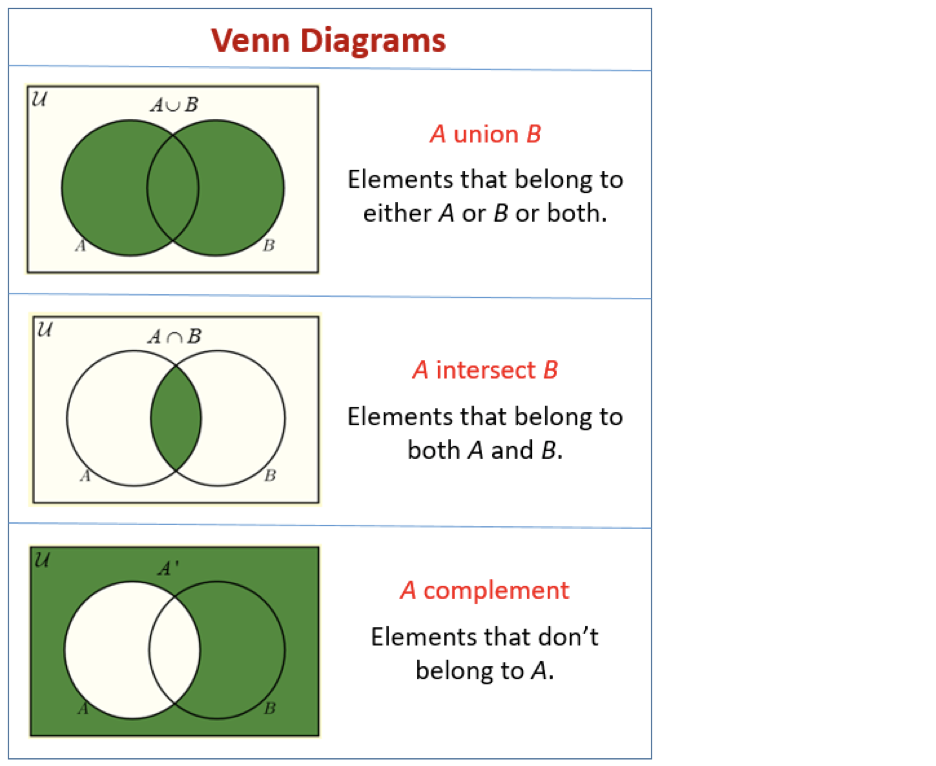
• A Venn diagram is a used to show the logical relation between sets. It was developed by John Venn in the 1880s.

Union, Intersection, and Complement

• The union of two sets contains all the elements contained in both sets. The union is notated A ⋃ B.
• The intersection of two sets contains only the elements that are in both sets. The intersection is notated A ⋂ B.
• The complement of a set A contains everything that is not in the set A. The complement is notated A'
• A universal set is a set that contains all the elements we are interested in. This would have to be defined by the context.
  (Refer venn diagram given ahead)

Illustration:
Consider the sets:
A = {red, green, blue}
B = {red, yellow, orange}
C = {red, orange, yellow, green, blue, purple}
Then,

• The union contains all the elements in either set:

  • A ⋃ B = {red, green, blue, yellow, orange} Notice we only list red once.

• The intersection contains all the elements in both sets: A ⋂ B = {red}

• Suppose the universal set is U = all whole numbers from 1 to 9.
  Then, If A = {1, 2, 4}, then A’ = {3, 5, 6, 7, 8, 9}.

Venn Diagram

• A ⋃ B =(A) +(B) – (A ⋂ B)
• A U B U C = (A) + (B) + (C) - (A ∩ B) - (B ∩ C) - (A ∩ C) + (A ∩ B ∩)

Check out our CSAT Course

Practice Questions:

1. There are 20000 people living in Defence Colony, Gurgaon. Out of them 9000 subscribe to Star TV Network and 12000 to Moon TV Network. If 4000 subscribe to both, how many do not subscribe to any of the two?
a. 3000
b. 2000
c. 4000
d. 1000

2. At the birth party of Pranav, a baby boy, 40 persons chose to kiss him and 25 chose to shake hands with him. 10 persons chose to both kiss him and shake hands with him. How many persons turn out at the party?
a. 35
b. 75
c. 55
d. 25

3. A class has 175 students. The following data shows the number of students obtaining one or more subjects. Mathematics 100, Physics 70, Chemistry 40; Mathematics and Physics 30, Mathematics and Chemistry 28, Physics and Chemistry 23; Mathematics, Physics and Chemistry 18. How many students have offered Mathematics alone
a. 35
b. 48
c. 60
d. 22

4. In a town of 10,000 families it was found that 40% family buy newspaper A, 20% buy newspaper B and 10% families buy newspaper C, 5% families buy A and B, 3% buy B and C and 4% buy A and C. If 2% families buy all the three newspapers, then number of families which buy A only is
a. 3100
b. 3000
c. 3300
d. 4100

5. In a battle 70% of the combatants lost one eye, 80% an ear, 75% an arm, 85% a leg, x% lost all the four limbs. The minimum value of x is
a. 10
b. 12
c. 15
d. None of these

6. In a class of 30 pupils, 12 take needle work, 16 take physics and 18 take history. If all the 30 students take at least one subject and no one takes all three then the number of pupils taking 2 subjects is
a. 16
b. 6
c. 8
d. 20

7. In a city 20 percent of the population travels by car, 50 percent travels by bus and 10 percent travels by both car and bus. Then persons travelling by car or bus is
a. 80%
b. 40%
c. 60%
d. 70%

8. 20 teachers of a school either teach mathematics or physics. 12 of them teach mathematics while 4 teach both the subjects. Then the number of teachers teaching physics only is
a. 12
b. 8
c. 16
d. None of these

9. In a group of 60 people, 27 like cold drinks and 42 like hot drinks and each person likes at least one of the two drinks. How many like both coffee and tea?
a. 8
b. 10
c. 9
d. 26

10. In a test in which 120 students appeared, 90 passed in history, 65 passed in Sociology and 75 passed in political science. 30 students in only one subjects and 55 students in only 2. 5 students no subjects. How many students passed in all the 3 subjects?
a. 25
b. 30
c. 35
d. Data insufficient

Log-in to access answers for Set Theory and other topics!

If you have made it so far, well done. You are ahead of the competition.

Best of luck!