Table of contents
CSAT can make or break your attempt!
This has been never more evident than from the 2023 prelims cut-off!
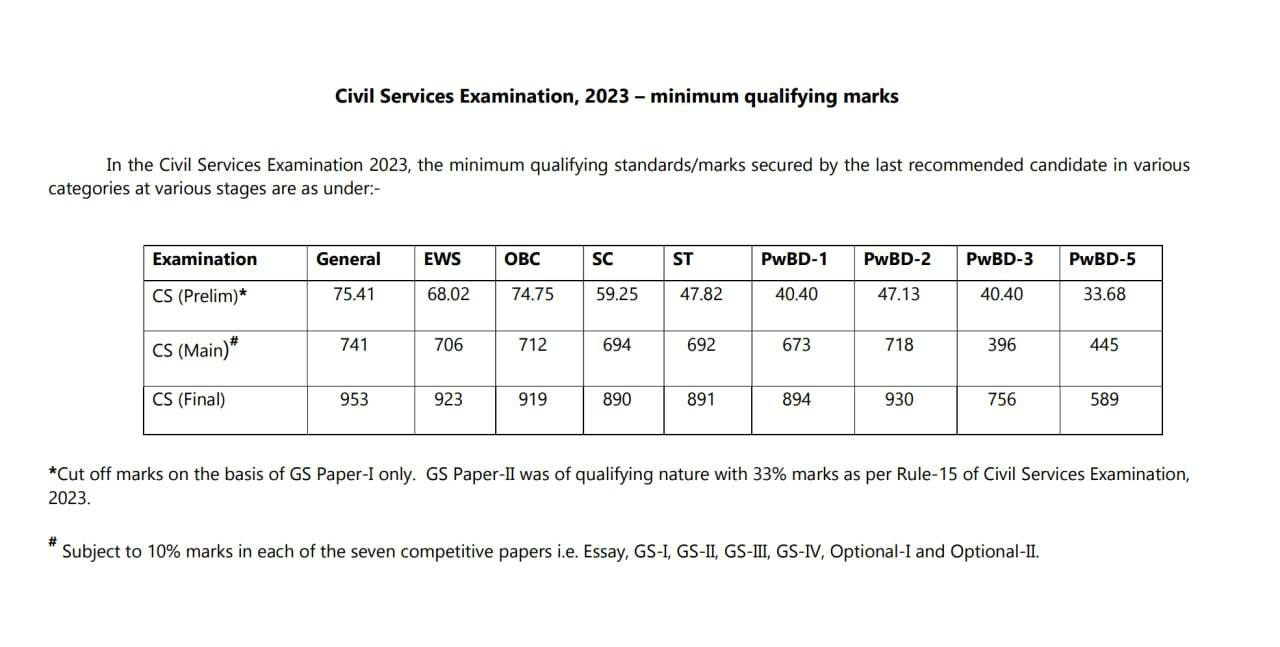
Therefore, lets not take CSAT lightly anymore.
Join our Telegram Group!
Because we will post 5 GS and 2 CSAT PYQs everyday on our Telegram Group to help you revise 10 years worth of UPSC questions.
"Click Here" to solve GS Questions.
Proceed to Solve CSAT MCQs.👇
Let's get solving...

Day 1 - (23 April 2024)
Q.1) A group of 630 children is seated in rows for a group photo session. Each row contains three less children than the row in front of it. Which one of the following number of rows is not possible? (2014)
(a) 3
(b) 4
(c) 5
(d) 6
Solution: (d)
Let no of children be x, x + 3, x + 6, x+ 9, x +12, x+ 15 ...........
And these children are in Rows - R1, R2, R3, R4, R5, R6….
Rows given as 3, 4, 5, 6.. So putting these values-
When R = 3;
x+x+3+x+6 = 630; 3x+9= 630; 3x= 621; x= 207
When R = 4;
x+x+3+x+6+x+9= 630; 4x+18= 630; 4x= 612; x= 153
When R= 5;
x+x+3+x+6+x+9+x+12= 630; 5x+ 30= 630; 5x= 600; x= 120
When R = 6;
x+x+3+x+6+x+9+x+12+x+15 = 630; 6x+45 = 630; 6x = 585; X = 97.5
Because x is not an integer. So, R = 6 is the answer.
Q.2) If Sohan while selling two goats at the same price , makes a profit of 10% on one goat and suffers a loss of 10% on the other one (2014)
(a) He makes no profit, no loss.
(b) He makes a profit of 1%.
(c) He suffers a loss of 1%.
(d) He suffers a loss of 2%.
Solution: (c)
If profit and loss percent on two different items is equal, then there will always be a loss.
Simply putting values in the formula - we get
% final loss = (%loss * % gain)/ 100 = (10 * 10/ 100) = 1% loss.

Day 2 - (24 April 2024)
Q.3) In a row ‘A’ is in the 11th position from the left and B is in the 10th position from the right. If ‘A’ and ‘B’ interchange then A becomes 18th from the left. How many persons are there in the row other than A and B ?
(2014)
(a) 27
(b) 26
(c) 25
(d) 24
Solution: (c)
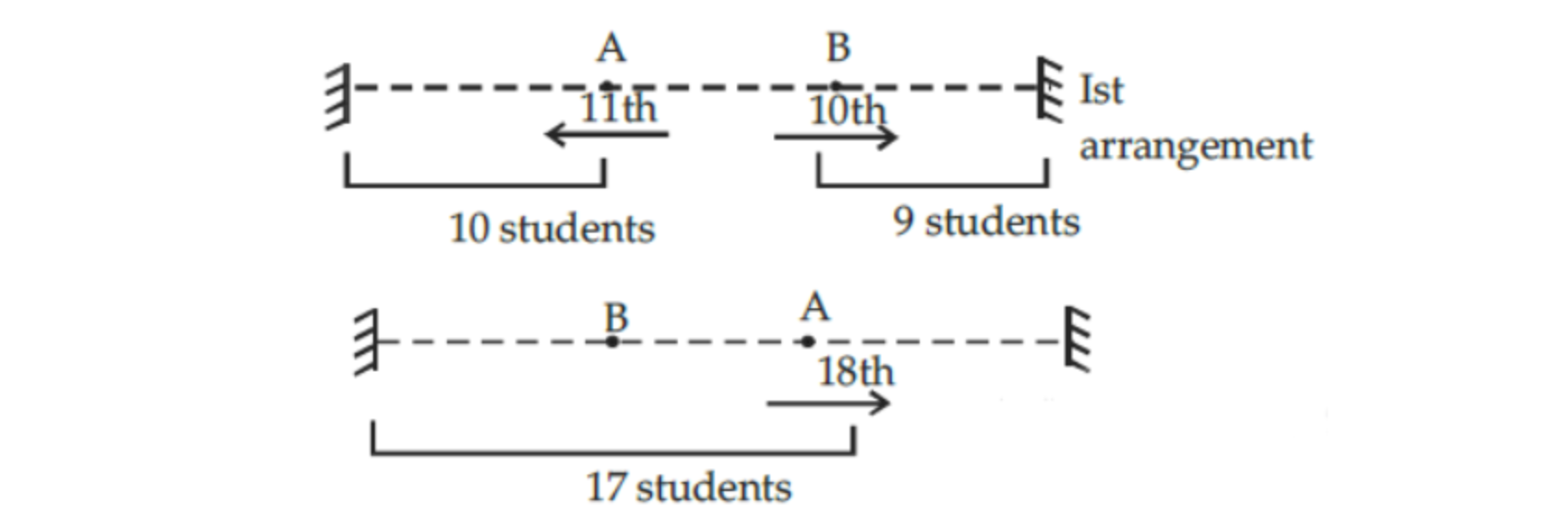
No. of students between A and B in the 1st arrangement = 17 - 11 = 6.
Total no. of students except A and B is = 10 + 6 + 9 = 25
Q.4) Location of B is north of A and the location of C is east of A. The distances AB and AC are 5 km and 12 km respectively. The shortest distance in km between the locations B and C is- (2014)
(a) 60
(b) 13
(c) 17
(d) 7
Solution: (b)
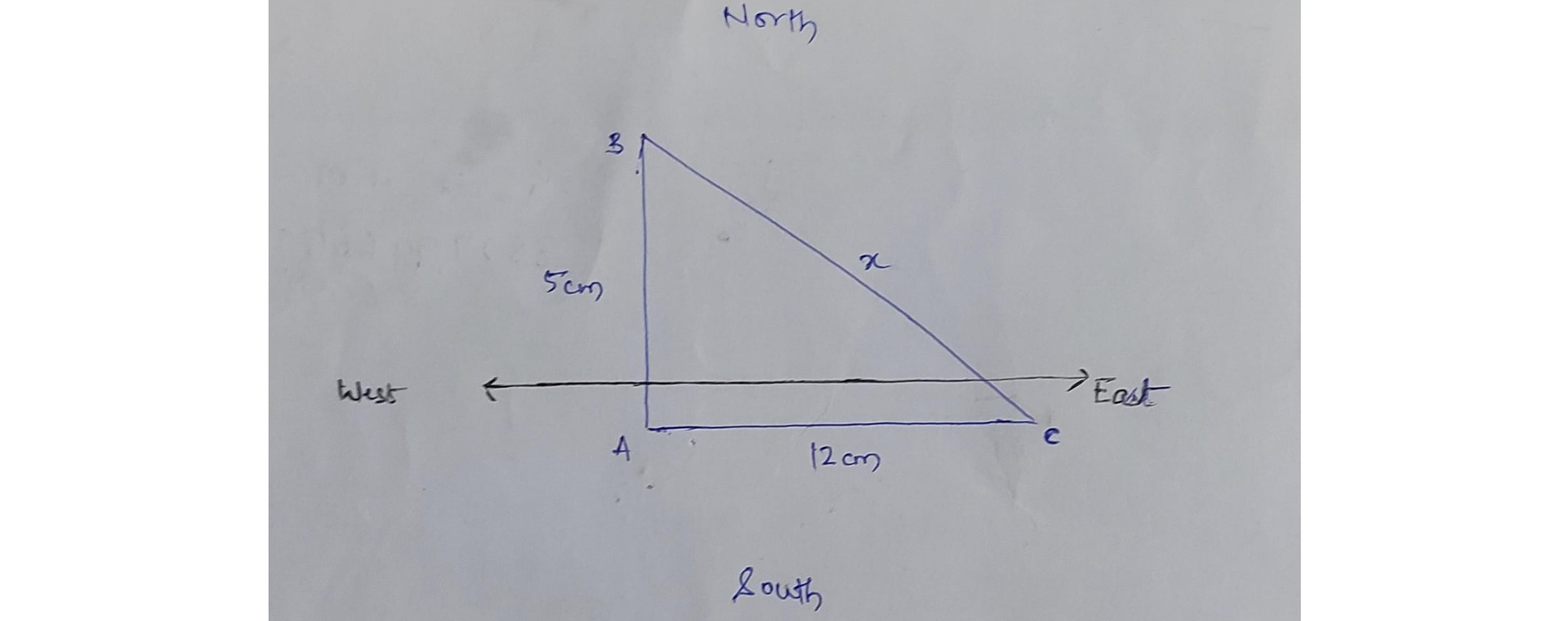
To find the distance between B and C, a right triangle is considered where AB and AC are the sides and BC is the hypotenuse.
Applying the Pythagorean theorem, the shortest distance BC is found to be 13 km.


Day 3 - (25 April 2024)
Q.1) Five persons fire bullets at a target at an interval of 6, 7, 8, 9 and 12 seconds, respectively. The number of times they would fire the bullets together at the target in an hour is - (2014)
(a) 6
(b) 7
(c) 8
(d) 9
Solution: (b)
To find out the time gap after which they will first hit the target, calculate the LCM of 6 7 8 9 12.
LCM = 504 sec
∴ In 1 hr = 3600 sec
No. of time they will hit together is 3600/504 = 7 times in an hour.
Q.2) There are seven persons up on a ladder A B C D E F and G not in that order. A is further up than E but is lower than C. B is in the middle. G is between A and B. E is between B and F. If F is between E and D the person on the bottom step of the ladder will be - (2014)
(a) B
(b) F
(c) D
(d) E
Solution: (c)
As per the given information, B is in the middle.
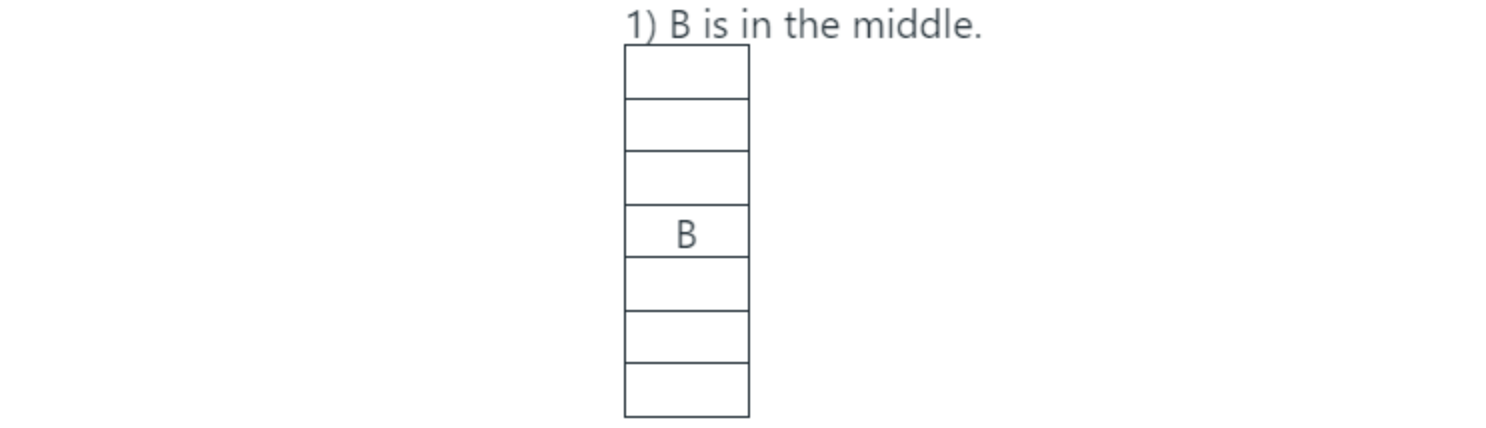
Other information -
A is further up than E but is lower than C.
G is between A and B.
E is between B and F.
F is between E and D.
This means that there is a vacancy in between A and B.
If A is two steps above B, G will be on the 5th step from bottom and C will be on the top most step. The resulting arrangement is-
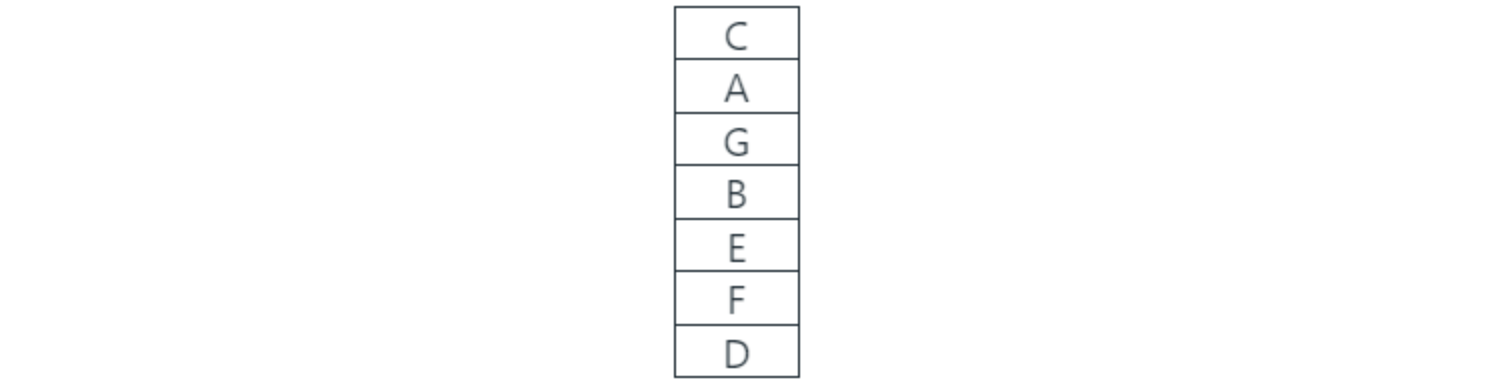
Hence, D is on the last step.

Day 4 - (26 April 2024)
Q. 1 A worker reaches his factory 3 minutes late if his speed from his house to the factory is 5 km/hr If he walks at a speed of 6 km/hr, then he reaches the factory 7 minutes early. The distance of the factory from his house is-
(2014)
(a) 3 km
(b) 4 km
(c) 5 km
(d) 6 km
Solution: (c)
Let the distance be x km,
x/5 - 3/60 = x/6 + 7/60
x/5 - x/6 = 10/60
x/30 = 1/6
x = 5 km
Q.2 Liberty therefore is never real unless the Government can be called to account when it invades rights.
Which one of the following is the best justification of the above statement ?
(2014)
(a) In the realization that the government can be brought to book in a court of law.
(b) In identifying a man as a political unit in a way which distinguishes him from other citizens.
(c) In a decentralized society wherein the basic needs of men can find satisfaction.
(d) In the understanding that liberty and restraints are complementary.
Solution: (d)
- In the understanding that liberty and restraints are complementary is the statement which best explains why Liberty therefore is never real unless the Government can be called to account when it invades rights.

Day 5 - (27 April 2024)
Q. 1 If the third day of a month is Monday, then which day of the week will be the fifth day from the 21st of that month? (2014)
(a) Monday
(b) Tuesday
(c) Wednesday
(d) Friday
Solution: (c)
3rd day ⇒ Monday
10th day ⇒ Monday
17th day ⇒ Monday
24th day ⇒ Monday
Fifth day from the 21st is the 26th day.
So the 26th day is Wednesday.
Q. 2 For a charity show, the total tickets sold were 420. Half of these tickets were sold at the rate of Rs. 5 each, one-third at the rate of Rs. 3 each and the rest for Rs.2 each. What was the total received? (CSE 2014)
(a) Rs. 900
(b) Rs.1540
(c) Rs.1610
(d) Rs.2000
Solution: (c)
Total tickets sold = 420
Half of the tickets sold at the rate of Rs. 5 each.
Therefore, 210 tickets sold = 210 × 5 = Rs 1050
One third ticket sold for Rs. 3 i.e 1/3 of 420 = 140 tickets sold at Rs. 3 each.
Collection through it = 140 × 3 = Rs 420
The Remaining 70 tickets were sold at the rate of Rs. 2 each.
So collection = 70 × 2 = Rs 140
Total collection = 1050 + 420 + 140 = 1610.


Day 6 - (29 April 2024)
Q.1 Two cars start towards each other, from two places A and B which are at a distance of 160 km. They start at the same time, 8:10 AM. If the speeds of the cars are 50 km and 30 km per hour respectively, they will meet each other at- (2014)
(a) 10:10 AM
(b) 10:30 AM
(c) 11:10 AM
(d) 11:20 AM
Solution: (a)
A --------------------X km--------------P -------------- (160−X) km-----------------B
Speed of B= 30 kmph
Let time taken to meet at point P Is the same as both trains started at the same time . Now,
Time taken to travel X km by A=X/50 .........(i)
Time taken to travel (160−X) km by B=(160−X)/30 ............(ii)
Comparing equation (i) and (ii), we have
X/50 = (160−X)/30 ⇒ 3X=800−5X ⇒8X=800 ⇒X=100 km
Time taken by A to travel 100 = 100/50=2 hours.
So, they will meet each other at 10:10 AM.
Q.2 Four persons Alok, Bhupesh, Chander and Dinesh have a total of Rs.100 among themselves. Alok and Bhupesh between them have as much money as Chander and Dinesh between them but Alok has more money than Bhupesh; and Chander has only half the money that Dinesh has. Alok has in fact Rs.5 more than Dinesh has. Who has the maximum amount of money? (2014)
(a) Alok
(b) Bhupesh
(c) Chander
(d) Dinesh
Solution: (a)
Alok + Bhupesh + Chander + Dinesh = Rs.100
Alok + Bhupesh = Chander + Dinesh
OR
Alok + Bhupesh = Chander + Dinesh = Rs.50
Also, 2Chander = Dinesh
Chander = Rs 16.67
Dinesh = Rs 33.33
Alok = 33.33 + 5 = 38.33
Bhupesh = 50 - 38.33 = Rs 11.67
So, Alok has the highest amount of money.

Day 7 - (30 April 2024)
Q. 1 The letters L, M, N, O, P, Q, R, S and T in their order, are substituted by nine integers 1 to 9 but not in that order. 4 is assigned to P. The difference between P and T is 5. The difference between N and T is 3. What is the integer assigned to N? (2014)
(a) 7
(b) 5
(c) 4
(d) 6
Solution: (d)
Given that P = 4 and T - P = 5
Also, T - N = 3.
Now, T - P = 5; T - 4 = 5; T = 9
And, 9 - N = 3; N = 6.
So N = 6.
Q.2 The number of deaths among the army personnel is 8 in 1000 but among the civilian population it is 20 per 1000. Which one of the following inferences can be drawn from this statement? (2014)
(a) It is better to join the army.
(b) The relationship is fortuitous.
(c) The Quality of Life Index is very high within the armed forces.
(d) The groups cannot be compared due to their heterogeneity.
Solution: (d)
- Army personnel go through training and are generally fit. While civilians are diverse which includes all age groups.
- Thus both are heterogenous and cannot be compared.

Day 8 - (1 May 2024)
Q.1 A and B decide to travel from place X to place Y by bus. A has Rs.10 with him and he finds that it is 80% of the bus fare for two persons. B finds that he has Rs. 3 with him and hands it over to A. In this context which one of the following statements is correct ? (CSE 2014)
(a) Now the money A has is just enough to buy two tickets.
(b) A still needs Rs2 for buying the tickets.
(c) After buying the two tickets A will be left with 50 paise.
(d) The money A now has is still not sufficient to buy two tickets.
Solution: (c)
A has Rs 10, and if B gives Rs.3 to A, now A has Rs.13
Cost of 2 tickets = 80% of x = 10
x= Rs 12.50
So, A is left with Rs.13 – 12.50 = 50 paise.
Q.2 As per agreement with a bank a businessman had to refund a loan in some equal installments without interest. After paying 18 installments he found that 60 percent of his loan was refunded. How many installments were there in the agreement ? (CSE 2014)
(a) 22
(b) 24
(c) 30
(d) 33
Solution: (c)
Let the amount in each installment be x
And total amount be a
Number of installments = Total amount / Amount in each installment
18 = (60/100) × a / x
18x = (60/100) x a
(18 × 100)/60 = (a/x)
a/x = 30
∴ Number of installments are 30

Day 9 - (2 May 2024)
Q.1 Consider that-
- A is taller than B
- C is taller than A.
- D is taller than C.
- E is the tallest of all. (CSE 2014)
If they are made to sit in the above order of their height, who will occupy the mid position?
(a) A
(b) B
(c) C
(d) D
Solution: (c)
- The sequence as per data-
Thus ‘C’ occupies the mid position.
Q.2 Consider the following statements-
There are six villages A B C D E and F.
- F is 1 km to the west of D.
- B is 1 km to the east of E.
- A is 2 km to the north of E.
- C is 1 km to the east of A.
- D is 1 km to the south of A. (CSE 2014)
Which three villages are in a line ?
(a) A C B
(b) A D E
(c) C B F
(d) E B D
Solution: (b)
- Drawing a diagram based on the statements given.
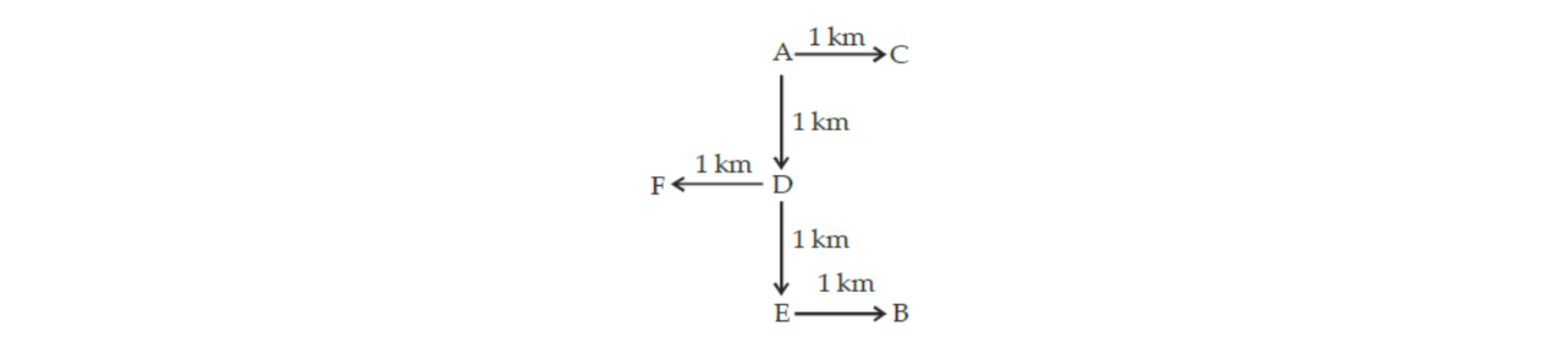
Hence ADE are in a line.

Day 10 - (3 May 2024)
Q.1 Four children are sitting in a row. A is occupying the seat next to B but not next to C. If C is not sitting next to D, who is/are occupying seat/seats adjacent to D ? (CSE 2014)
(a) B
(b) A
(c) B and A
(d) Impossible to tell
Solution: (b)
Exp: The description is used to draw the following arrangement.
Thus option b is correct.
Q.2 Assume that-
- The hour and minute hands of a clock move without jerking.
- The clock shows a time between 8 o'clock and 9 o'clock.
- The two hands of the clock are one above the other.
After how many minutes (nearest integer) will the two hands be again lying one above the other? (CSE 2014)
(a) 60
(b) 62
(c) 65
(d) 67
Solution: (c)
When the minute hand travels 60 minutes, the hour hand only travels 5 minutes.
The relative time between both hands = 60 - 5 = 55 minutes.
They would meet again after = 60/55 = 1.09 hours
1.09 hours = 1.09 × 60 = 65.4 minutes.
They would meet again after 65 minutes.


Day 11 - (4 May 2024)
Q.1 Twelve people form a club. By picking lots one of them will host a dinner for all once in a month. The number of dinners a particular member has to host in one year is- (CSE 2014)
(a) One
(b) Zero
(c) Three
(d) Cannot be predicted
Solution: (d)
- We cannot predict the number of dinners for a particular member from the given data.
- It is a possibility that by choosing members from picking lots, one may have to host a dinner more than once.
Q.2 What is the missing number in the series 7 X 21 31 43 ? (CSE 2014)
(a) 11
(b) 12
(c) 13
(d) 14
Solution: (c)
The difference increases by 2 units in each step.
7 + 6 = 13
13 + 8 = 21
21 + 10 = 31
31 + 12 = 43
Thus 13 is the missing number.

Day 12 - (6 May 2024)
Q.1 In a test, a candidate attempted only 8 questions and secured 50% marks in each of the questions. If he obtained a total of 40% in the test and all questions in the test carried equal marks, how many questions were there in the test? (CSE 2014)
(a) 8
(b) 10
(c) 15
(d) 16
Solution: (b)
Let each question carry x marks
The equation becomes-
8x * 50/100 = 40
x = 40/4
x = 10
Thus the number of questions in the test = 10
Q.2 A father is nine times as old as his son and the mother is eight times as old as the son. The sum of the father's and the mother's age is 51 years. What is the age of the son? (CSE 2014)
(a) 7 years
(b) 5 years
(c) 4 years
(d) 3 years
Solution: (d)
Sum of father's age and mother's age = 51 years
Let the age of the son is x
Father’s age = 9x and mother’s age = 8x
So, 9x + 8x = 51 years
⇒ 17x = 51 years
⇒ x = 3 years
The age of the son is 3 years.

Day 13 - (7 May 2024)
Q.1 Four persons A B C and D consisting of two married couples are in a group. Both the women are shorter than their respective husbands. A is the tallest among the four. C is taller than B. D is B's brother. In this context which one of the following statements is not correct ? (CSE 2015)
(a) All four have family ties.
(b) B is the shortest among the four.
(c) C is taller than D.
(d) A is B's husband.
Solution: (c)
Given information- A is the tallest among the four. Hence A is male.
D is also male as D is the brother of B.
Thus B and C are females.
D is the husband of C.
D is shorter than A but is taller than B.
Thus B is shorter from above. Thus option c is incorrect.
Q.2 If A runs less fast than B and B runs as fast but not faster than C; then as compared to A, C runs- (CSE 2015)
(a) Slower than A
(b) Faster than A
(c) With same speed as A
(d) Given data is not sufficient to determine
Solution: (b)
As per information, relative speeds give following inference- A < B < C
Now compared to A, C runs faster.

Day 14 - (8 May 2024)
Q.1 Consider the following statements:
- A man had a wife, two sons and daughters in his family.
- The daughters were invited to a feast and the male members of the family went out to take part in a picnic.
- The man's father did not return from his work. (CSE 2014)
Which of the following statements is true?
(a) Only the man's wife was left at home
(b) It is likely that the man's wife was left at home
(c) None was left at home
(d) More than one person was left at home
Solution: (b)
- It is given that all the male members of the family went out to take part in a picnic.
- Also, daughters were invited to a feast. But nothing is specified about the man's wife.
- Hence (b) statement that the man’s wife is likely to be left at home is true.
Q.2 Geeta: Naresh has become a better boxer since he started meditation.
Radha: Impossible. A boxer's most important asset is his aggressiveness.
Radha’s statement reflects her belief that- (CSE 2014)
(a) Meditation tends to make a person less aggressive.
(b) Meditation has little or no effect on the person who practices it.
(c) Naresh was a poor boxer earlier because he was not aggressive enough.
(d) Naresh would not have taken to meditation as he was a boxer.
Solution: (a)
- Radha did not accept the opinion that meditation makes a person a better boxer because boxing requires aggressiveness.
- Which implies that Radha believes that meditation makes a person less aggressive.

Day 15 - (9 May 2024)
Q.1 All good athletes want to win and all athletes who want to win eat a well-balanced diet; therefore all athletes who do not eat a well-balanced diet are bad athletes. The best conclusion from this statement is that
(a) No bad athlete wants to win.
(b) No athlete who does not eat a well-balanced diet is a good athlete.
(c) Every athlete who eats a well-balanced diet is a good athlete.
(d) All athletes who want to win are good athletes.
Solution: (b)
The given statements can be seen as:
- All good athletes want to win.
It does not mean that no one wants to win. Also, there can be people other than good athletes who eat a well balanced diet. Hence b is true.
Q.2 Each of A, B, C and D has Rs.100. A pays Rs. 20 to B who pays Rs.10 to C who gets Rs. 30 from D. In this context, which one of the following statements is not correct?
(a) C is the richest
(b) D is the poorest.
(c) C has more than what A and D have together.
(d) B is richer than D
Solution: (c)
According to question A B C and D each carry Rs.100. After the given transactions,
A has Rs 80
B has Rs 110
C has Rs 140
D has Rs 60
Here option c is not correct because C has more than what A and D have together.


Day 16 - (10 May 2024)
Q.1 In a town, 45% of the population read magazine A, 55% read magazine B, 40% read magazine C, 30% read magazines A and B, 15% read magazines B and C, 25% read magazines A and C and 10% read all the three magazines. What percentage do not read any magazine? (CSE 2015)
(a) 10%
(b) 15%
(c) 20%
(d) 25%
Solution: (c)
Number of population who read the magazine= 45 + 55 + 40 – 30 + 25 +15 + 10
= 140 – 70 + 10= 80%
Number of population who do not read magazine = 100 – 80 = 20%
Q.2 Examine the following statements: (CSE 2015)
- Lady finger is tastier than cabbage.
- Cauliflower is tastier than lady finger.
- Cabbage is not tastier than peas.
The conclusion that can be drawn from these statements is that-
(a) Peas are as tasty as lady fingers.
(b) Peas are as tasty as cauliflower and lady-finger.
(c) Cabbage is the least tasty of the four vegetables.
(d) Cauliflower is tastier than cabbage.
Solution: (c)
As per given information, Cauliflower > Lady finger > Cabbage.
Also, Peas > Cabbage. So, cabbage is the least tasty among the four vegetables.

Day 17 - (11 May 2024)
Q.1 Shahid and Rohit start from the same point in opposite directions. After each 1 km Shahid always turns left and Rohit always turns right. Which of the following statements is correct ? (CSE 2015)
(a) After both have traveled 2 km the distance between them is 4 km.
(b) They meet after each has traveled 3km.
(c) They meet for the first time after each has traveled 4 km.
(d) They go on without ever meeting again.
Solution: (b)
Let's understand with a diagrammatic representation-
Their positions after each traveled as per given directions shows that both meet after having traveled 3 km.
Q.2 In a 500 meters race, B starts 45 meters ahead of A but A wins the race while B is still 35 meters behind. What is the ratio of the speeds of A to B assuming that both start at the same time? (CSE 2015)
(a) 25: 21
(b) 25: 20
(c) 5:3
(d) 5:7
Solution: (a)
Total distance = 500 meter
Distance covered by A= 500 meter
Distance covered by B = 500 – 45 – 35 = 500 – 80 = 420
Ratio= 500:420 = 25:21

Day 18 - (13 May 2024)
Q.1 Two equal glasses of the same type are respectively 1/3 and 1/4 full of milk. They are then filled up with water and the contents are mixed in a pot. What is the ratio of milk and water in the pot?
(a) 7 : 17
(b) 1 : 3
(c) 9 : 21
(d) 11 : 23
Solution: (a)
Let the capacity of each of the glass be x liter.
Then, Each glass contains x/3l and x/4l of milk.
Therefore- x/3 + x/4 = 4x+3x/ 12 = 7x/10 liter
So, the quantities of water in the first and the second glasses were
(x-x/3)liter and (x-x/4)liter
After simplifying, 2x/3 + 3x/4 = 8x+9x/12 = 7x/12
The ratio of milk and water is = 7x/12 : 17x/12 = 7:17
Q.2 Out of 130 students appearing in an examination, 62 failed in English, 52 failed in Mathematics, whereas 24 failed in both English and Mathematics. The number of students who passed finally is-
(a) 40
(b) 50
(c) 55
(d) 60
Solution: (a)
Total students = 130
Total students failed = 62 + 52 – 24= 114 – 24= 90
Number of students passed finally = 130 – 90 = 40

Day 19 - (14 May 2024)
Q.1 In a group of persons traveling in a bus, 6 persons can speak Tamil, 15 can speak Hindi and 6 can speak Gujarati. In that group none can speak any other language. If 2 persons in the group can speak two languages only and one person can speak all the three languages then how many persons are there in the group? (CSE 2015)
(a) 21
(b) 22
(c) 23
(d) 24
Solution: (c)
Let a be the one who speaks one language
Let b be the one who speaks two languages
Let c be the one who speaks three languages,
Then
a + 2b + 3c = 6 +15 +6
a + 4 + 3 = 27
a = 20.
Thus total number of persons in the group = 20 + 2 + 1 = 23.
Q.2 In a parking area, the total number of wheels of all the cars (four-wheelers) and scooters/motorbikes (two wheelers) is 100 more than twice the number of parked vehicles. The number of cars parked is - (CSE 2015)
(a) 35
(b) 45
(c) 50
(d) 55
Solution: (c)
Let number of cars be x
Let number of scooters / motorbikes = y
So, total number of parked vehicles = x + y
Now according to question, 4x + 2y = 2 x + y + 100;
4x + 2y = 2x + 2y + 100;
2x = 100x = 50
Hence the number of cars parked is 50.

Day 20 - (15 May 2024)
Q.1 The mangroves can shed tons of leaves per acre every year; fungi and bacteria break down this leaf litter and consume it, they then are consumed by tiny worms and crustaceans which in turn feed small fish which feed larger fish and birds and crocodiles. Which among the following is the most logical inference of the above statement? (CSE 2015)
(a) Coastal areas cannot have food chains without mangroves.
(b) Mangroves are an essential component of all marine ecosystems.
(c) Mangroves have a crucial role in some of the coastal food chains.
(d) The composition of marine flora and fauna is largely determined by mangroves.
Solution: (c)
- The passage indicates the role Mangroves play in some of the coastal food chains. There are many other food chains that might exist with or without Mangroves. So, (c) is correct.
Q.2 By liberty I mean the eager maintenance of that atmosphere in which men have the opportunity to be their best selves. Which one of the following expresses the view implied in the above statement? (CSE 2015)
(a) Liberty is the absence of restraint on human action.
(b) Liberty is what law permits people to perform.
(c) Liberty is the ability to do what one desires.
(d) Liberty is the maintenance of conditions for the growth of human personality.
Solution: (d)
- As per the option A, liberty means the eager maintenance of that atmosphere which might require restrictions as well which makes it wrong.
- Option b says that if the people work only according to the law they might become good citizens but might not work to their best selves thus it is wrong.
- Option c is wrong because it promotes materialist thinking which is not the best self.
- Option d is correct because with the growth of human personality the people would be their best selves.


Day 21 - (16 May 2024)
Q.1 A selection is to be made for one post of Principal and two posts of Vice-Principal. Amongst the six candidates called for the interview only two are eligible for the post of Principal while they all are eligible for the post of Vice-Principal. The number of possible combinations of selectees is- (CSE 2015)
(a) 4
(b) 12
(c) 18
(d) None of the above
Solution: (d)
As per given data,
Number of ways to select Principal = 2C1
Number of ways to select Vice Principal = 5C2
Total number of ways = 2C1 + 5C2
Number of possible combinations of selectres = 2 × 10 = 20
Q.2 A student has to opt for 2 subjects out of 5 subjects for a course namely Commerce, Economics, Statistics, Mathematics I and Mathematics II. Mathematics II can be offered only if Mathematics I is also opted. The number of different combinations of two subjects which can be opted is- (CSE 2015)
(a) 5
(b) 6
(c) 7
(d) 8
Solution: (c)
If mathematics I is not opted, then two subjects out of four subjects have to be opted.
∴ Number of ways in which two subjects can be opted If mathematics II is opted because it can be opted only if mathematics I is also opted.
Number of ways in which two subjects can be opted for = 6 +1 = 7.

Day 22 - (17 May 2024)
Q.1 A person ordered 5 pairs of black socks and some pairs of brown socks. The price of a black pair was thrice that of a brown pair. While preparing the bill, the bill clerk interchanged the number of black and brown pairs by mistake which increased the bill by 100%. What was the number of pairs of brown socks in the original order? (CSE 2015)
(a) 10
(b) 15
(c) 20
(d) 25
Solution: (d)
Suppose, The number of a pairs of brown socks = y
Price of brown socks = x
So the price of black socks = 3x
As per the question ⇒ 5 * 3x + xy = 100
If the price is increased by 100%
So the pairs of brown socks = 25
Q.2 The number of persons who read magazine X only is thrice the number of persons who read magazine Y. The number of persons who read magazine Y only is thrice the number of persons who read magazine X. Then which of the following conclusions can be drawn?
1. The number of persons who read both the magazines is twice the number of persons who read only magazine X.
2. The total number of persons who read either one magazine or both the magazines is twice the number of persons who read both the magazines. (CSE 2015)
Select the correct answer using the code given below:
(a) 1 only
(b) 2 only
(c) Both 1 and 2
(d) Neither 1 nor 2
Solution: (c)
Understanding and solving with a venn diagram.
Number of people who read only magazine X = A
Number of people who read only magazine Y = C
Number of people who read both magazines = B
Thus, 3A = B + C and 3C = B + A
Substituting wrt B;
3A - C = 3C - A
4A = 4C
A = C
Substituting A = C in the first two equations, B = 2A = 2C = A + C
The number of people who read both the magazines are twice the number of people who read only magazine X.
The number of people who either read only one magazine or both magazines
= B + (A + C) = B + B = 2B
Therefore, the total number of people who either read one magazine or both magazines is twice the number of persons who read both magazines.
Both conclusions are true.

Day 23 - (18 May 2024)
Q.1 Each of the six different faces of a cube has been coated with a different color i.e. V I B G Y and O. Following information is given: (CSE 2015)
- Colors Y O and B are on adjacent faces.
- Colors I G and Y are on adjacent faces.
- Colors B G and Y are on adjacent faces.
- Colors O V and B are on adjacent faces.
Which is the color of the face opposite to the face coloured with O?
(a) B
(b) V
(c) G
(d) I
Solution: (c)
From statements 2 and 3, I and B are on opposite faces.
From statements 1 and 4, Y and V are adjacent to O.
Therefore, G is the color of the face opposite to the face coloured with O.
Q.2 Two pipes A and B can independently fill a tank completely in 20 and 30 minutes respectively. If both the pipes are opened simultaneously, how much time will they take to fill the tank completely? (CSE 2015)
(a) 10 minutes
(b) 12 minutes
(c) 15 minutes
(d) 25 minutes
Solution: (b)
Time taken by A and B is 20 and 30 min respectively to fill a tank.
Work = time × efficiency
Total work = LCM of 20 and 30 = 60
Efficiency of pipe A = 60/20 = 3
Efficiency of pipe B = 60/30 = 2
Efficiency when both work together = 3 + 2 = 5
So, total time = 60/5 = 12 minutes.
So, Both A and B will take time to fill the tank completely together is 12 min.

Day 24 - (20 May 2024)
Q.1 Consider the following statements followed by two conclusions: (CSE 2015)
Statements : Some men are great.
: Some men are wise.
Conclusion I : Men are either great or wise.
Conclusion II : Some men are neither great nor wise.
Which one of the following is correct?
(a) Only conclusion I is valid.
(b) Only conclusion II is valid.
(c) Both the conclusions are valid.
(d) Neither of the conclusions is valid.
Solution: (d)
- Understanding with a venn diagram.
It shows that both the conclusions do not hold true.
Q.2 Consider the following statements: (CSE 2015)
1. Some claim to have seen UFOs Unidentified Flying Objects.
2. Life on other heavenly bodies is considered to be a possibility.
3. Voyage to space is now an established fact.
From the above statements it may be concluded that-
(a) UFOs are heavenly bodies
(b) UFOs are sent from other heavenly bodies
(c) Some living species in other heavenly bodies are more intelligent than man
(d) Nothing definite can be said about the UFOs
Solution: (d)
- As per the statements, life on other heavenly bodies might be possible but it is not a surety. And though some people claim to have seen UFOs, it is not an accepted or proven thing.

Day 25 - (21 May 2024)
Q.1 Usha runs faster than Kamala Priti runs slower than Swati Swati runs slower than Kamala. Who is the slowest runner? (CSE 2015)
(a) Kamala
(b) Priti
(c) Swati
(d) Usha
Solution: (b)
According to question-
Relative Speeds-> Priti < Swati < Kamala < Usha.
Thus it can be concluded that PRITI is the slowest runner.
Q.2 If ABC × DEED = ABCABC; where A, B, C, D and E are different digits, what are the values of D and E? (CSE 2015)
(a) D = 2, E = 0
(b) D = 0, E = 1
(c) D = 1, E = 0
(d) D = 1, E = 2
Solution: (c)
When we write any Number in form of ABCABC, that number must be divisible by 13, 11 and 7. Also, ABCABC is multiple of 1001
So, 1001 = DEED
1001 = 13 × 11 × 7
ABC × DEED = ABC
ABC ⇒ ABC × 1001 = ABC ABC
On comparing D = 1, E = 0


Day 26 - (22 May 2024)
Q.1 Between 6 PM and 7 PM the minute hand of a clock will be ahead of the hour hand by 3 minutes at- (CSE 2015)
(a) 6: 15 PM
(b) 6: 18 PM
(c) 6: 36 PM
(d) 6: 48 PM
Solution: (c)
Between 6 PM and 7 PM, the minute hand and the hour hand coincide at 6 hr ‘m’ minutes.
Thus, the hour hand and minute hand coincide at 6 hr 32 8/11 mins.
Now, after 3 minutes i.e. at 6 : 36 PM the minute hand of a clock will be ahead of the hour hand by 3 minutes.
Q.2 There are 5 tasks and 5 persons. Task-l cannot be assigned to either person-l or person-2. Task-2 must be assigned to either person-3 or person-4. Every person is to be assigned one task. In how many ways can the assignment be done? (CSE 2015)
(a) 6
(b) 12
(c) 24
(d) 144
Solution: (c)
Given - 5 persons and 5 tasks.
Condition I, When task T2 is given to person 3
No of ways for Task T1= 2
For Task 2 = 1
For Task 3 = 3
For Task 4 = 3
For Task 5 = 3
Total no. of ways for condition = 3 + 3 + 3 + 2 + 1 = 12
Condition II, When task T2 is given to be person 4
No. of ways for Task T1 = 2
For Task T2 = 1
For Task T3 = 3
For Task T4 = 3
For Task T5 = 3
Total number of ways for condition II= 3 + 3 + 3 + 2 +1 = 12
Total number of ways for conditions I and II = 12 + 12 = 24

Day 27 - (23 May 2024)
Q.1 The monthly incomes of Peter and Paul are in the ratio of 4 ∶ 3. Their expenses are in the ratio of 3 ∶ 2. If each saves Rs.6,000 at the end of the month, their monthly incomes respectively (in Rs.) are ? (CSE 2015)
(a) 24,000 and 18,000
(b) 28,000 and 21,000
(c) 32,000 and 24,000
(d) 34,000 and 26,000
Solution: (a)
Given data, Peter and Paul’s income ratio = 4 :3
Peter and Paul’s Expense = 3 : 2
Now-> Saving = income – expense
Saving of each = 6000 Rs
Income = 4x : 3x
Expense = 3y : 2y
Equations
⇒ 4x -3y = 6000 —(1)
⇒ 3x – 2y = 6000 —(2)
By solving (1) and (2), we get x = y = 6000
So, the income of Peter is 4x = 4 × 6000 = 24000 Rs.
The income of Paul is 3x = 3 × 6000 = 18000 Rs.
Q.2 Two cities P and Q are 360 km apart from each other. A car goes from P to Q with a speed of 40km per hour and returns back to P with a speed of 50 km per hour. Whta is the average speed of the car? (CSE 2015)
(a) 44.44 km per hour
(b) 48 km per hour
(c) 50 km per hour
(d) 55 km per hour
Solution: (a)
Distance between the two cities = 360 km
Formula:
Average speed = Total distance/Total time
Distance = Speed × Time
So,
Time taken by car A to cover distance from P to Q = 360/40 = 9 hours
Time taken by car A to cover distance from Q to P = 360/50 = 7.2 hours
Average speed = (360 + 360)/(9 + 7.2) = 44.44 km/hr

Day 28 - (24 May 2024)
Q.1 In a society it is customary for friends of the same sex to hug and for friends of opposite sex to shake hands when they meet. A group of friends met in a party and there were 24 handshakes. Which one among the following numbers indicates the possible number of hugs? (CSE 2015)
(a) 39
(b) 30
(c) 21
(d) 20
Solution: (c)
Let number of women be x
Let number of men be y
Total number of hand shakes = xy = 24
Possible factors of x and y become ->
x = 6 or 4, y = 4 or 6
Q.2 Two men, Anil and David, and two women, Shabnam and Rekha are in a sales group. Only two speak Tamil. The other two speak Marathi. Only one man and one woman can drive a car. Shabnam speaks Marathi. Anil speaks Tamil. Both Rekha and David can drive. Which of the following statements is true? (CSE 2015)
(a) Both the Tamil speakers can drive a car.
(b) Both the Marathi speakers can drive a car.
(c) Both of those who can drive a car speak Marathi.
(d) One of those who can drive a car speaks Tamil
Solution: (d)
From the below table, it can be seen that only those who can drive a car can speak Tamil.

Day 29 - (25 May 2024)
Q.1 In a plane, line X is perpendicular to line Y and parallel to line Z; line U is perpendicular to both lines V and W; line X is perpendicular to line V. Which one of the following statements is correct? (CSE 2015)
(a) Z, U and W are parallel.
(b) X, V and Y are parallel.
(c) Z, V and U are all perpendicular to W.
(d) Y, V and W are parallel.
Solution: (d)
The figure indicates that Y, V and W are parallel.
Q.2 A cow costs more than 4 goats but less than 5 goats. If a goat costs between Rs. 600 and Rs. 800 which of the following is a most valid conclusion? (CSE 2015)
(a) A cow costs more than Rs 2 500.
(b) A cow costs less than Rs.3 600.
(c) A cow costs between Rs.2 600 and Rs.3 800.
(d) A cow costs between Rs. 2 400 and Rs.4 000.
Solution: (d)
Let ‘g’ be the cost of goats.
4g < Cow < 5g
Now, if goat price= Rs 600
2400 < Cow < 3000
If goat price= Rs 800
3200 < Cow < 4000
Hence, it can be seen that cow cost is between Rs. 2400 and Rs. 4000.

Day 30 - (27 May 2024)
Q.1 A ate grapes and pineapple; B ate grapes and oranges; C ate oranges pineapple and apple; D ate grapes apple and pineapple. After taking fruits B and C fell sick. In the light of the above facts it can be said that the cause of sickness was- (CSE 2016)
(a) Apple
(b) Pineapple
(c) Grapes
(d) Oranges
Solution: (d)
A → Grapes and Pineapple
B → Grapes and Oranges
C → Oranges, Pineapple, and Apple
D → Grapes, Apple, and Pineapple
Because only B and C fell sick, oranges were the fruit that only B and C ate.
Q.2 A person X was driving in a place where all roads ran either north-south or east-west, forming a grid. Roads are at a distance of 1 km from each other in a parallel. He started at the intersection of two roads, drove 3 km north, 3 km west and 4 km south. Which further route could bring him back to his starting point, if the same route is not repeated? (CSE 2016)
(a) 3 km east, then 2 km south
(b) 3 km east, then 1 km north
(c) 1 km north, then 2 km west
(d) 3 km south, then 1 km north
Solution: (b)
X starts from point A and passes through point B and C and reaches point D.
X returns from point D, passes through point E and reaches point A back.
Thus, the answer is 3 km east, then 1 km north.


Day 31 - (28 May 2024)
Q.1 Consider the following statement
"We shall go either for a picnic or for trekking".
Which of the following, if true, would falsify this claim? (CSE 2016)
(a) We go for a picnic but not for trekking
(b) Activities such as picnics and trekking are encouraged by the health
(c) We go for trekking and not for picnic
(d) We do not go either for picnic or for trekking
Solution: (d)
"We shall go either for a picnic or for trekking".
Option 4 i.e ‘We do not go either for picnics or for trekking’ is against both and if this statement is true, it would falsify the statement given in the question.
Q.2 There were 50 faculty members comprising 30 males and the rest females. No male faculty member knew music, but many of the female faculty members did. The Head of the institution invited six faculty members to a tea party by lottery. At the party it was discovered that no member knew music. The conclusion is that: (CSE 2016)
(a) The party comprised male faculty members only.
(b) The party comprised only those female faculty members who could not give renderings in music.
(c) The party comprised both male and female faculty members.
(d) Nothing can be said about the gender composition of the party.
Solution: (d)
- The question does not say anything about the gender composition of the group invited for the party. And there is no conclusive statement on which specific female faculty know music.
- So either all in the party were males, or some males and some females who did not know music were present in the party.

Day 32 - (29 May 2024)
Q.1 Five people A, B, C, D and E are seated about a round table. Every chair is spaced equidistant from adjacent chairs. (CSE 2016)
(i) C is seated next to A
(ii) A is seated two seats from D
(iii) B is not seated next to A.
On the basis of the above information, which of the following must be true?
- D is seated next to B
- E is seated next to A
- D and C are separated by two seats.
Select the correct answer using the code given below:
(a) 1 only
(b) 1 and 2 only
(c) 3 only
(d) Neither 1 nor 2 nor 3
Solution: (b)
The arrangement is in a circular table.
C is seated next to A
Conclusion : A - C or C - A
C is seated two seats from D
Conclusion : A – D or D – A
B is not seated next to A
Conclusion : E must be next to A
Combining, A C D B E
So, only statements 1 and 2 are correct
Q.2 There are five hobby clubs in a college viz, photography, yachting, chess, electronics and gardening. The gardening group meets every second day, the electronics group meets every third day, the chess group meets every fourth day, the yachting group meets every fifth day and the photography group meets every sixth day. How many times do all the five groups meet on the same day within 180 days? (CSE 2016)
(a) 3
(b) 5
(c) 10
(d) 18
Solution: (a)
LCM. of 2, 3, 4, 5, 6 = 60
So, all five hobby clubs meet every 60th day.
In a period of 180 days, they meet thrice i.e. on 60th, 120th and 180th day.

Day 33 - (30 May 2024)
Q.1 There are some nectar-filled flowers on a tree and some bees are hovering on it. If one bee lands on each flower, one bee will be left out. If two bees land on each flower, one flower will be left out. The number of flowers and bees respectively are- (CSE 2016)
(a) 2 and 4
(b) 3 and 2
(c) 3 and 4
(d) 4 and 3
Solution: (d)
Suppose, the number of bees = x
Then the number of flowers = (x - 1)
If the number of bees sitting on each flower is 2,
The number of flowers is (x/2 + 1).
Now solving
⇒ (x/2 + 1) = (x - 1)
⇒ x - x/2 = 2
⇒ x/2 = 2
⇒ x = 4
Therefore, the number of bees is 4 and the number of flowers is (4 - 1) i.e. 3.
Q.2 There is an order of 19000 quantity of a particular product from a customer. The firm produces 1000 quantities of that product per day out of which 5% are unfit for sale. In how many days will the order be completed? (CSE 2016)
(a) 18
(b) 19
(c) 20
(d) 22
Solution: (c)
Total Order = 19000
Product produced every day = 1000
Percentage = (actual/Total) × 100
Calculation
⇒ Quantity of product to be completed = 19000
⇒ Actual production per day = 1000 - 5% of 1000 = 1000 - 50 = 950
⇒ No. of days to completed the order = 19000/950 = 20 days

Day 34 - (31 May 2024)
Q.1 A class starts at 11:00 am and lasts till 2:27 pm. Four periods of equal duration are held during this interval. After every period, a rest of 5 minutes is given to the students. The exact duration of each period is: (CSE 2016)
(a) 48 minutes
(b) 50 minutes
(c) 51 minutes
(d) 53 minutes
Solution: (a)
Class starts at 11:00 am and ends at 02:27 pm
Total duration of class = 3h 27min = 207 min
Of the 4 periods, after every period there is a 5 min break.
So, the duration of the periods = 207 – 3×5 = 192 min.
Time assigned to each period = 192/4 =48 min
Q.2 30g of sugar was mixed in 180 ml water in a vessel A, 40 g of sugar Was mixed in 280 ml of water in vessel B and 20 g of sugar was mixed in 100 ml of water in vessel C. The solution in vessel B is- (CSE 2016)
(a) Sweeter than that in C
(b) Sweeter than that in A
(c) As sweet as that in C
(d) Less sweet than that in C
Solution: (d)
30g sugar mixed in 180ml water in Vessel A
So, the concentration of sugar in vessel A is 30/180 g/ml i.e ⅙ g/ml
40g sugar mixed in 280 ml water in Vessel B
So, the concentration of sugar in vessel B is 40/280 g/ml i.e 1/7 g/ml
20g sugar mixed in 100ml water in Vessel C
So, the concentration of sugar in vessel C is 20/100 g/ml i.e ⅕ g/ml
More sugar concentration means more sweetness.
Therefore, sweetness : C > A > B

Day 35 - (1 June 2024)
Q.1 In aid of charity, every student in a class contributes as many rupees as the number of students in that class. With the additional contribution of Rs.2 by one student only, the total collection is Rs. 443. Then how many students are there in the class? (CSE 2016)
(a) 12
(b) 21
(c) 43
(d) 45
Solution: (b)
Let the number of students in the class be x.
Total collection without considering the additional contribution by one student = 443 – 2 = Rs.441
Number of students in the class are 21.
Q.2 Anita’s mathematics test had 70 problems carrying equal marks i.e., 10 arithmetic, 30 algebra and 30 geometry. Although she answered 70% of the arithmetic, 40% of the algebra and 60% of the geometry problems correctly, she did not pass the test because she got less than 60% marks. The number of more questions she would have to answer correctly to earn a 60% passing marks is: (CSE 2016)
(a) 1
(b) 5
(c) 7
(d) 9
Solution: (b)
Questions correctly answered are:-
Arithmetic – 70% of 10 = 7
Algebra – 40% of 30 = 12
Geometry – 60% of 30 = 18
Total questions correctly answered = 7 + 12 + 18 = 37
Anita had to attempt 60% of 70 questions i.e., 42 questions correctly to pass the test. Number of more questions required to be answered = 42 – 37 = 5


Day 36 - (3 June 2024)
Q.1 In a class, there are 18 very tall boys. If these constitute three-fourths of the boys and the total number of boys is two-thirds of the total number of students in the class, what is the number of girls in the class? (CSE 2016)
(a) 6
(b) 12
(c) 18
(d) 21
Solution: b
No. of boys who are very tall are 18
Let the total number of boys be x.
⇒ (3/4)x = 18
⇒ x = 18 × (4/3) = 24.
If the total number of students is y,
⇒ (2/3) y = 24
⇒ y = 24 x (3/2) = 36.
So the number of girls in the class = (36 - 24) = 12.
Q.2 Consider the following statements: (CSE 2016)
- Either A and B are of the same age or A is older than B
- Either C and D are of the same age or D is older than C
- B is older than C
Which of the following conclusions can be drawn from the above statements?
(a) A is older than B
(b) B and D are of the same age
(c) D is older than C
(d) A is older than C
Solution: d
Statements can be represented in terms of mathematical inequalities:
1) Either A and B are of the same age or A is older than B. ⇒ A ≥ B
2) Either C and D are of the same age or D is older than C. ⇒ D ≥ C
3) B is older than C. ⇒ B > C
Combining ⇒ A ≥ B > C; D ≥ C
In these options, only A greater than C is definite.

Day 37 - (4 June 2024)
Q.1 Two numbers X and Y are respectively 20% and 28% less than a third number Z. By what percentage is the number Y less than the number X? (CSE 2016)
(a) 8 %
(b) 9 %
(c) 10 %
(d) 12 %
Solution: c
Given: Two numbers X and Y are 20% and 28% less than a third number Z.
Let the value of Z be 100
X is 20% less than the third number ⇒ 100 × (100 - 20)/100
⇒ 80 Y is 28% less than the third number
⇒ 100 (100 - 28)/100 ⇒ 72
According to the question,
⇒ {(X - Y)/X}× 100
⇒ {(80 - 72)/80}× 100 ⇒ 10%
∴ The number Y less than the number X is 10%.
Q.2 A daily train is to be introduced between station A and station B starting from each at 6 AM and the journey is to be completed in 42 hours. What is the number of trains needed in order to maintain the Shuttle Service? (CSE 2016)
(a) 2
(b) 3
(c) 4
(d) 7
Solution: c
- The figures below show that train 1 leaves station A and train 2 leaves station B on the first day.
- Both trains don’t reach their destination even after 24 hours on the second day, as the journey completes in 42 hours.
- Two more trains need to be introduced at both stations, station A and B. Thus, four trains are needed to maintain the shuttle service.

Day 38 - (5 June 2024)
Q.1 How many zeroes are there at the end of the following product?
1 × 5 × 10 × 15 × 20 × 30 × 35 × 40 × 45 × 50 × 55 × 60 (CSE 2020)
(a) 10
(b) 12
(c) 14
(d) 15
Solution: a
5 × 2 is a must to get a zero. Let's find the number of 2's and 5's
⇒ 1 × 5 × 10 × 15 × 20 × 30 × 35 × 40 × 45 × 50 × 55 × 60
There are only 4 2's and 6 5's.
We need both 2 and 5 to get a 0.
So, only 4 new zeros are added to 6.
Number of zeros = 4 + 6 = 10
There will be 10 zeros.
Q.2 Let XYZ be a three-digit number, where (X + Y + Z) is not a multiple of 3. Then (XYZ + YZX + ZXY) is not divisible by- (CSE 2020)
(a) 3
(b) 9
(c) 37
(d) (X + Y + Z)
Solution: b
XYZ is a three-digit number, where (X + Y + Z) is not a multiple of 3.
General form of a number XYZ = X × 100 + Y × 10 + Z
Calculation:
The general form of XYZ = 100X + 10Y + Z.
The general form of YZX = 100Y + 10Z + X
The general form of ZXY = 100Z + 10X + Y.
Adding the three numbers, we get;
⇒ XYZ + YZX + ZXY = (100X + 10Y + Z) + (100Y + 10Z + X) + (100Z + 10X + Y)
⇒ XYZ + YZX + ZXY = 111X + 111Y + 111Z
⇒ XYZ + YZX + ZXY = 111(X + Y + Z).
Now, it is clear that 111 is the common factor.
So, XYZ + YZX + ZXY is divisible by 111 and its factors.
Factors of 111 are 3 and 37.
That eliminates options 3 and 37.

Day 39 - (6 June 2024)
Q.1 Let p, q, r and s be natural numbers such that p - 2016 = q + 2017 = r - 2018 = s + 2019 Which one of the following is the largest natural number? (CSE 2020)
(a) P
(b) Q
(c) R
(d) S
Solution: c
The equation - p - 2016 = q + 2017 = r - 2018 = s + 2019
Let s =1
⇒ r - 2018 = s + 2019
⇒ r = 2020 + 2018 = 4038
⇒ q + 2017 = r - 2018
⇒ q + 2017 = 4038 - 2018
⇒ q = 3
⇒ p - 2016 = q + 2017
⇒ p - 2016 = 3 + 2017
⇒ p = 4036
⇒ p - 2016 = q + 2017 = r - 2018 = s + 2019
⇒ 4036 - 2016 = 3 + 2017 = 4038 - 2018 = 1 + 2019
⇒ 2020 = 2020 = 2020 = 2020
Condition satisfied p = 4036, q = 3, r = 4038, s = 1
∴ r = 4038 is the largest number.
Q.2 How many five - digit prime numbers can be obtained by using all the digits 1, 2, 3, 4 and 5 without repetition of digits? (CSE 2020)
(a) Zero
(b) One
(c) Nine
(d) Ten
Solution: a
For finding prime numbers, we will use the divisibility rule.
Divisibility rule of:-
2 = last number should be multiple of 2.
3 = sum of digits should be divisible by 3.
4 = last 2 digits should be multiple of 4.
5 = last digit should be 0 or 5.
6 = should follow the divisibility rule of 2 and 3.
We can arrange the number as we want so we can check the last digit rule later.
Start with divisibility of 3 ⇒ 1 + 2 + 3 + 4 + 5 = 15
And 15 is divisible by 3.
So, any combination of the numbers gives us sum of 15 that will not be a prime number.
So, there is no such combination of 1, 2, 3, 4 and 5 that will give us a prime number.

Day 40 - (7 June 2024)
Q.1 If you have two straight sticks of length 7.5 feet and 3.25 feet, what is the minimum length can you measure? (CSE 2020)
(a) 0.05 foot
(b) 0.25 foot
(c) 1 foot
(d) 3.25 foot
Solution: b
Lengths of sticks are 7.5 feet and 3.25 feet.
Formula: HCF of (A/B) and (C/D) = (HCF of A and C)/(LCM of B and D)
⇒ 7.5 = 75/10 = 15/2
⇒ 3.25 = 325/100 = 13/4
Now, minimum length will be measured by HCF of {15/2, 13/4}
⇒ HCF = 1/4 = 0.25
∴ The minimum length that can be measured by two sticks is 0.25 feet.
Q.2 One page is torn from a booklet whose pages are numbered in the usual manner starting from the first page as 1. The sum of the numbers on the remaining pages is 195. The torn page contains which of the following numbers? (CSE 2020)
(a) 5, 6
(b) 7, 8
(c) 9, 10
(d) 11, 12
Solution: b
The sum of the numbers on the remaining pages is 195.
But there is a page that is torn up.
Sum of 1st n natural numbers = (n/2)(n + 1)
So, we consider the sum of the number of pages in book be x
So, the total sum will be 195 + x
So, 195 + x = (n/2)(n + 1)
At n = 19, sum of pages will be 190 so this cannot be considered.
Now at 20, sum of pages = 210
[(20/2) × 21 = 210)
So the number of pages must be 20
Now we can assume that
195 + x = 210 ⇒ x = 15
Here in option be the sum of pages is 15 (page 7 and 8)

Day 41 - (8 June 2024)
Q.1 Consider the following arrangement that has some missing letters: abab_b_bcb_dcdcded_d The missing letters which complete the arrangement are-
(a) a, b, c, d
(b) a, b, d, e
(c) a, c, c, e
(d) b, c, d, e
Solution: c
The pattern is a b a b a / b c b c b / c d c d c /d e d e d.
Hence, a, c, c, e is the correct answer.
Q.2 If in a particular year 12th January is a Sunday, then which one of the following is correct?
(a) 15th July is a Sunday if the year is leap year.
(b) 15th July is a Sunday if the year is not a leap year
(c) 12th July is a Sunday if the year is a leap year.
(d) 12th July is not a Sunday if the year is a leap year.
Solution: c
Number of days between 12th January to 12th July in a leap year.
= 19 + 29 + 31 + 30 + 31 + 30 + 12 = 182 = 26 weeks
Hence, 12th July will be Sunday, the same day as 12th January in a leap year.

Day 42 - (10 June 2024)
Q.1 A family of two generations consisting of six members P, Q, R, S, T and U has three males and three females. There are two married couples and two unmarried siblings. U is P's daughter and Q is R's mother-in-law. T is an unmarried male and S is a male. Which one of the following is correct? (CSE 2020)
(a) R is U's husband
(b) R is S's wife.
(c) S is unmarried.
(d) None of the above
Solution: b
As it is a family of two generations P, Q belong to the first generation and U, R belong to the second generation.
T, S are male and U, Q are females.
T is an unmarried male. The possible family tree is
Hence, R is S's wife.
Q.2 A man walks down the backside of his house straight 25 meters, then turns to the right and walks 50 meters again; then he turns towards left and again walks 25 meters. If his house faces to the East, what is his direction from the starting point? (CSE 2020)
(a) South-East
(b) South-West
(c) North-East
(d) North-West
Solution: d
Man's final position is in the North-West with respect to his starting point.
Previous Post
